Character Table

A character table is a mathematical description of the symmetry operations for a point group. The numbers in the table (called characters) are mathematical results of the transformations of points caused by the symmetry operations. The set of irreducible representations is unique to each point group and can be used to define the molecule. The math behind these tables is quite complex and a detailed description is not given here. For more information, refer to Chemical Applications of Group Theory by F. Albert Cotton, Interscience Publishers, 1963.

The SymApps application can compute all types of character tables, except the infinite ones (C(inf)v, D(inf)h, and R3). For the point groups described by Cn, Cnv, Cnh, Dn, Dnd, Dnh, and Sn, the variable n can be up to 255.

Do one of the following to create a character table:

• Click on the Standard toolbar.

• Choose Compute > Character Table.

The Compute Character Table dialog box opens:

• Enter the character table symbol (e.g. D6h, Ih) in the text box.

• Check Convert Complex Entries to Real Values if you want SymApps to convert complex table entries to real values. This option only applies to the character tables of Cn, Cnh, Sn, T, and Th. However, it is recommended that you leave complex entries as they are, because you may get erroneous results when the reduction formula is used. See the Reduce Reducible Representation topic.

The character table opens in its own tab.

A sample character table for D5h is explained below.

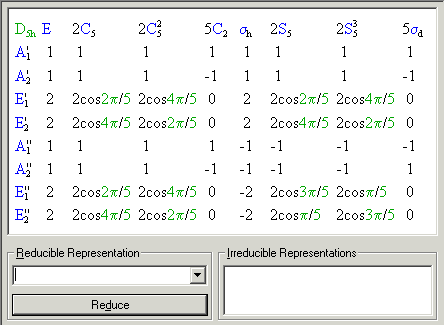
The value in the top-left corner (D5h) is the point group name. The values across the top are the symmetry operations for the group, which are categorized into conventional classes. Each class defines its own column. The values down the left are the symbols (called Mulliken symbols) for the irreducible representations that distinguish each row as a set of characters for each symmetry operation. That is to say, since the transformation in a symmetry operation can be represented mathematically in many ways, and since the math can be reduced, there is a finite number of irreducible representations that uniquely defines each point group. These irreducible representations are given in each row of the table.  

If you have calculated another representation and want to see how it reduces to one of those given in the character table, choose Compute > Reduce Reducible Representation.